helper functions for potential evapotranspiration (ET0)
ET0_helper.Rdlambda: latent heat of vaporization, about[2.5 MJ kg-1].slope: The slope of the saturation vapour pressure curve at certain air temperatureTair,[kPa degC-1].gamma: psychrometric constant ([kPa degC-1]),Cp*Pa/(epsilon*lambda).U2: 10m wind speed (m/s). According to wind profile relationship, convert U_z to U_2.es: saturation vapor pressure (kPa)ea: actual vapor pressure (kPa)RH_mean|Tmin,Tmax:(es(Tmax) + es(Tmin)) * RH_mean/200Tmin:es(Tmin)
cal_TvK: vitual temperature (K)Tair + q
Tair + ea/Pa
1.01 * (Tair + 273), FAO56 Eq. 3-7
cal_rho_a: air density (kg/m^3)rH: resistance of aerodynamic (s/m), about100 s/m.
cal_U2(Uz, z.wind = 10)
cal_ea(Tmin, Tmax = NULL, RH_mean = NULL)
cal_VPD(Tair, Tdew = NULL)
cal_lambda(Tair)
cal_slope(Tair)
cal_gamma(Tair, Pa = atm)
cal_bowen(Tair, Pa = atm)
cal_Pa(z = NULL)
cal_rH(U2, h = 0.12)
cal_rH2(U2, Tair, Pa = atm)
cal_TvK(Tair, q = NULL, ea = NULL, Pa = atm)
cal_rho_a(Tair, Pa = atm, q = NULL, ea = NULL)
cal_es(Tair)Arguments
- Uz
wind speed at height
z.wind- z.wind
Height where measure the wind speed
[m]. Default 10m.- Tmin
Daily minimum air temperature at 2m height
[deg Celsius]- Tmax
Daily maximum air temperature at 2m height
[deg Celsius]- RH_mean
daily mean relative humidity
[%]- Tair
2m air temperature, (
[deg Celsius])- Tdew
dew temperature, (
[deg Celsius])- Pa
land surface Air pressure
[kPa].- z
Elevation above sea level
[m]. Must provided if pres are not provided.- U2
wind speed at 2m
- h
canopy height (m), for the calculation of the following intermediate variables:
d: zero plane displacement height (m)z_om: roughness length governing momentum transfer (m)z_oh: roughness length governing transfer of heat and vapour (m)z_h: height of humidity measurements (m)z_m: height of wind measurements (m)
- q
specific humidity (g/g)
- ea
actual vapor pressure (kPa)
References
Allen, R. G., & Luis S. Pereira. (1998). Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. European Journal of Agronomy, 34(3), 144–152. doi:10.1016/j.eja.2010.12.001
Examples
cal_VPD(10, 5)
#> [1] 0.3556517
par(mfrow = c(2, 2), mar = c(3, 1.8, 2, 1), mgp = c(2, 0.6, 0))
Tair <- -10:50
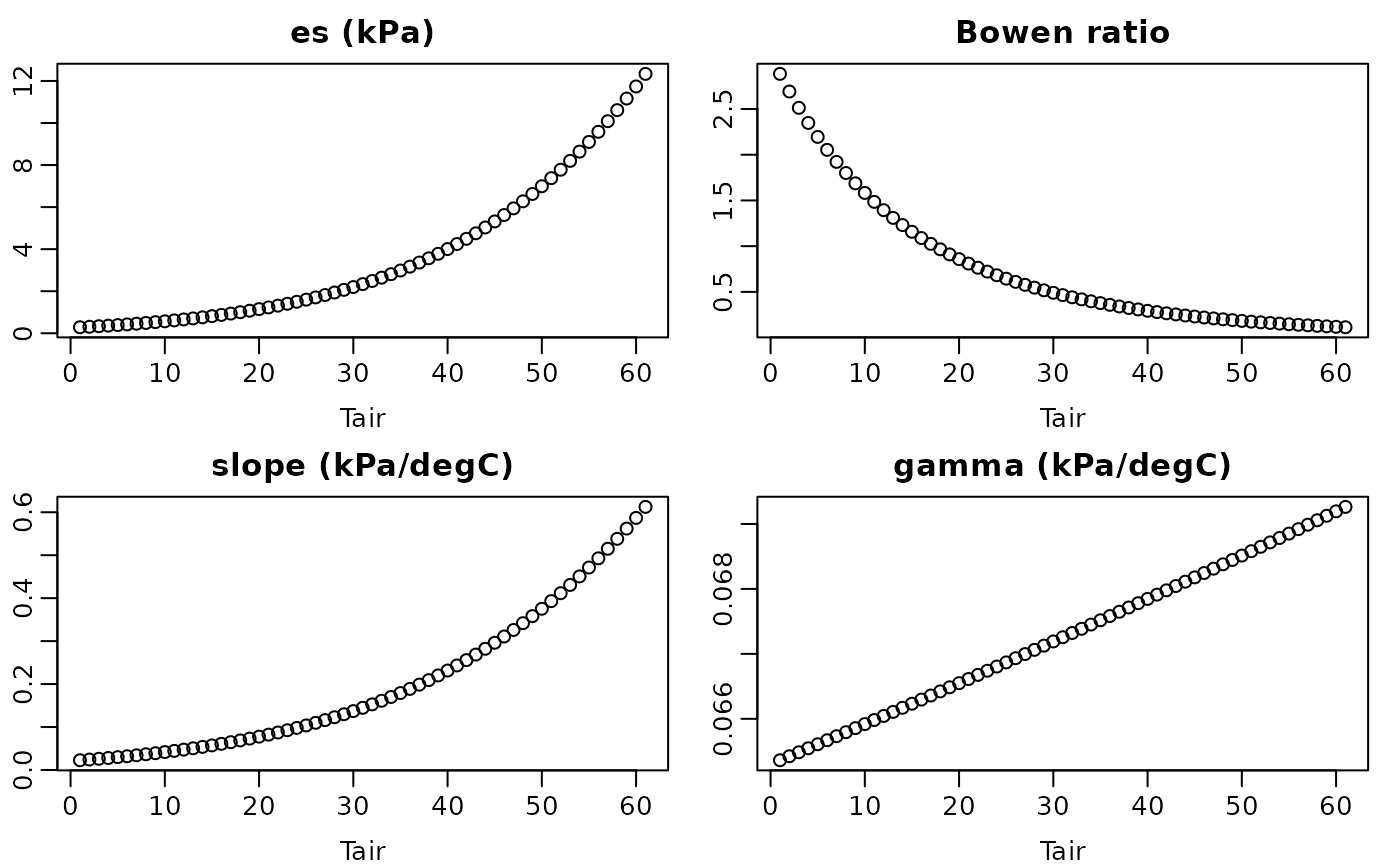
plot(cal_es(-10:50), main = "es (kPa)", xlab = "Tair")
plot(cal_bowen(-10:50), main = "Bowen ratio", xlab = "Tair")
plot(cal_slope(-10:50), main = "slope (kPa/degC)", xlab = "Tair")
plot(cal_gamma(-10:50), main = "gamma (kPa/degC)", xlab = "Tair")