1. 优化函数SCEUA率定模型参数 • hydroTools

下文以最简单的一元线性回归模型为例，展示了如何采用优化的方法率定模型参数。该方法完全可以移植、应用于复杂模型的参数优化（如马斯京根、蒸发模型、水文模型的参数率定）。读者可自行触类旁通。

谢宇轩&孔冬冬

1. 模型函数与输入数据

library(hydroTools)
library(ggplot2)

# simulation function
# ' @author [Yuxuan Xie](xieyx@cug.edu.cn)
fun_predict <- function(x, par) {
  x * par[1] + x * par[2]
}

#' Goal function
#' 
#' Find the parameter corresponding to the minimum value of the objective function
#' 
#' @note we need the index, the smaller, the better.
goal <- function(par, x, yobs, ...) {
  ysim = fun_predict(x, par) # ysim with the par
  hydroTools::GOF(yobs, ysim)$RMSE # one of -NSE, -KGE, RMSE
}

set.seed(1) # Ensure the random numbers generated each time are consistent
n = 50
x = 1:n
par = c(0.5, 2) # real parameter
yobs = par[1]*x + par[2] + rnorm(n, 1) # 实际应用过程中，yobs是已经提供的

fun_predict(x, par) # test above function
#>  [1]   2.5   5.0   7.5  10.0  12.5  15.0  17.5  20.0  22.5  25.0  27.5  30.0
#> [13]  32.5  35.0  37.5  40.0  42.5  45.0  47.5  50.0  52.5  55.0  57.5  60.0
#> [25]  62.5  65.0  67.5  70.0  72.5  75.0  77.5  80.0  82.5  85.0  87.5  90.0
#> [37]  92.5  95.0  97.5 100.0 102.5 105.0 107.5 110.0 112.5 115.0 117.5 120.0
#> [49] 122.5 125.0
goal(par, x, yobs)
#> [1] 55.93361

2. 参数优化

par_u = c(6, 6)   # upper boundary of par
par_l = c(-1, -1) # lower boundary of par
par0 = c(1, 1)    # initial parameter

# 这里以sceua为例展示如何进行参数优化，其他优化函数可以自行触类旁通
opt = rtop::sceua(goal, par = par0, lower = par_l, upper = par_u, 
  x = x, yobs = yobs, # other parameters passed to `goal`
  maxn = 1e3) 
#> 51 best 1.84 function convergence 200 parameter convergence 7610.145 
#> 79 best 1.76 function convergence 200 parameter convergence 4530.619 
#> 105 best 1.75 function convergence 200 parameter convergence 2690.471 
#> 131 best 1.74 function convergence 200 parameter convergence 2931.736 
#> 159 best 1.74 function convergence 200 parameter convergence 3057.855 
#> 184 best 1.74 function convergence 5.71 parameter convergence 2478.465 
#> 209 best 1.74 function convergence 1.09 parameter convergence 2314.297 
#> 234 best 1.74 function convergence 0.354 parameter convergence 1532.078 
#> 259 best 1.74 function convergence 0.000384 parameter convergence 1725.886 
#> 284 best 1.74 function convergence 0.000384 parameter convergence 1725.886 
#> 309 best 1.74 function convergence 2.79e-06 parameter convergence 1397.07 
#> 335 best 1.74 function convergence 4.28e-08 parameter convergence 976.0489 
#> 361 best 1.74 function convergence 4.28e-08 parameter convergence 452.3405 
#> 387 best 1.74 function convergence 1.32e-08 parameter convergence 355.4915 
#> 414 best 1.74 function convergence 6.81e-11 parameter convergence 309.5118 
#> 441 best 1.74 function convergence 1.96e-11 parameter convergence 345.5275 
#> 469 best 1.74 function convergence 2.19e-12 parameter convergence 356.8678 
#> 501 best 1.74 function convergence 8.92e-13 parameter convergence 238.4948 
#> 535 best 1.74 function convergence 7.65e-14 parameter convergence 312.2249 
#> 562 best 1.74 function convergence 2.55e-14 parameter convergence 247.6701 
#> 595 best 1.74 function convergence 2.55e-14 parameter convergence 253.8331 
#> 622 best 1.74 function convergence 0 parameter convergence 253.8331 
#> 650 best 1.74 function convergence 0 parameter convergence 296.1607 
#> 677 best 1.74 function convergence 0 parameter convergence 220.8968 
#> 704 best 1.74 function convergence 0 parameter convergence 196.6364 
#> 731 best 1.74 function convergence 0 parameter convergence 196.6364 
#> 756 best 1.74 function convergence 0 parameter convergence 196.6364 
#> 781 best 1.74 function convergence 0 parameter convergence 196.6364 
#> 806 best 1.74 function convergence 0 parameter convergence 196.6364 
#> 835 best 1.74 function convergence 0 parameter convergence 196.6364 
#> 865 best 1.74 function convergence 0 parameter convergence 196.6364 
#> 890 best 1.74 function convergence 0 parameter convergence 200.6591 
#> 920 best 1.74 function convergence 0 parameter convergence 196.6364 
#> 953 best 1.74 function convergence 0 parameter convergence 196.6364 
#> 982 best 1.74 function convergence 0 parameter convergence 196.6364 
#> 1008 best 1.74 function convergence 0 parameter convergence 196.6364
par_opt = opt$par # SCEUA生成的最优参数

3. 结果展示

ysim = fun_predict(x, par_opt)
dat = data.frame(x, yobs, ysim)

xx = seq(min(x), max(x), 0.1) # xsim
yy = fun_predict(xx, par = par_opt)

GOF(dat$yobs, dat$ysim)
#> # A tibble: 1 × 11
#>       R   pvalue    R2   NSE   KGE  RMSE   MAE   Bias Bias_perc    AI n_sim
#>   <dbl>    <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl>     <dbl> <dbl> <int>
#> 1 0.994 4.96e-47 0.987 0.942 0.841  1.74  1.45 -0.756   -0.0477 0.988    50

if (require(gg.layers)) {
  # remotes::install_github("rpkgs/gg.layers")
  suppressWarnings({
    p = ggplot(dat, aes(yobs, ysim)) + 
      geom_point() + 
      stat_gof(show.line = TRUE)
    print(p)
  })
  # Ipaper::write_fig(p, "Figure1_calib_lm.pdf", 6, 5)
} else {
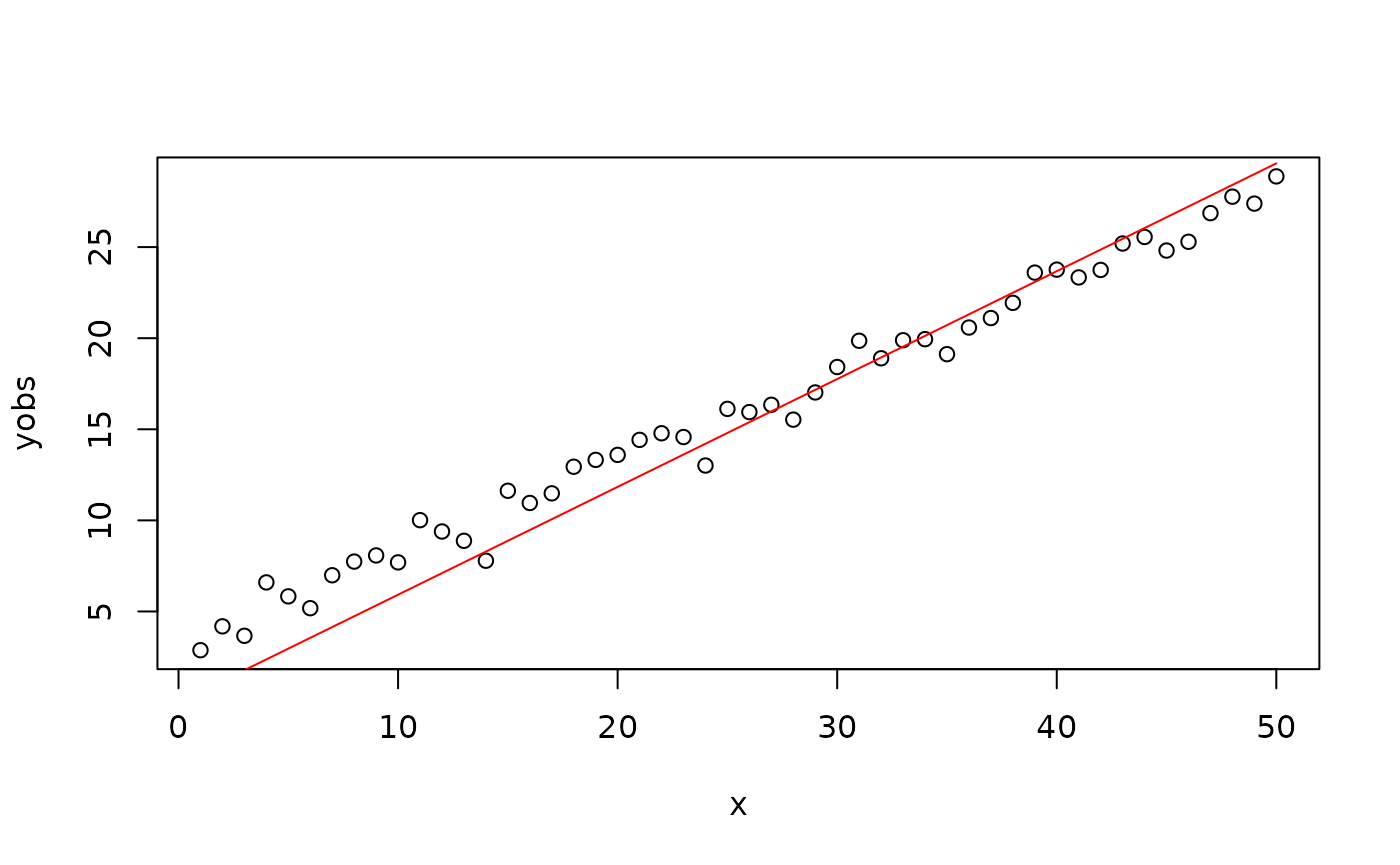
  plot(x, yobs)
  lines(xx, yy, col = "red")
}
#> Loading required package: gg.layers
#> Warning in library(package, lib.loc = lib.loc, character.only = TRUE,
#> logical.return = TRUE, : there is no package called 'gg.layers'